Símbolo de un potenciómetro.

Introducción

Los potenciómetros... ¿por qué no podían ser todos iguales?. Sería todo mucho más fácil. Vamos, ¡digo yo!. Pues no es así, qué le vamos a hacer.

Estos componentes son resistencias variables. Son los "mandos giratorios" de cualquier aparato electrico: Volumen, Graves, Agudos, Balance, Ganancia etc. Como son resistencias tienen el mismo sistema de medida que estas: Ohmios.

Los de carcasa de plástico son los más comunes y baratos, pero no son demasiado buenos por regla general. Los que llevan carcasa metálica suelen ser de mejor calidad. Además se puede soldar un cable de masa al "bote" del potenciómetro, del mismo modo que se hace en los potenciómetros de las guitarras.

Potenciómetro metálico.
Un buen potenciómetro metálico "Piher". Son un poco más caros pero merecen la pena.

Los hay de muuuuchos tipos diferentes, pero los que nos interesan por quí son básicamente los de 300º de giro (unos 270º útiles) y de dos tipos fundamentalmente:

• Lineales
• Logarítmicos (también llamados "de audio")

En principio, un potenciómetro es Lineal cuando el recorrido del cursor es proporcional a su valor en ohmios. Al 50% del recorrido es un 50% del valor, etc. Uno logarítmico, sin embargo, tiene una equivalencia asimétrica con respecto al recorrido, formando una curva que suele tener forma exponencial o logarítmica. Esto es así a causa de la "Ley Estímulo-Reacción de Fechner", en la que se demostró que el oído humano no tiene una respuesta lineal a las variaciones de volumen, sino que responde al logaritmo de la amplitud. Esto es, para que percibamos un sonido como "el doble de fuerte" que otro, ha de tener diez veces más volumen. Para ello necesitamos controles de volumen que actúen de manera similar y en los que la variación de amplitud sea muy pequeña al principio y muy grande al final. Esta propiedad de ciertos potenciómetros se conoce como "Ley de Variación" o "Taper" en inglés y en nuestro caso, necesitamos una "Variación Positiva" más comunmente conocida como Potenciómetro Logarítmico o "de Audio".

Lo peor del asunto es que, para mayor confusión, los fabricantes no se ponen de acuerdo en la demominación de cada tipo, así he visto potes de tipo "A", que normalmente son de "Audio" como lineales y potes de tipo "B" que son lineales o logarítmicos. Piher denomina a los logarítmicos como "Log" ó "B" es su serie metálica como el de la primera foto de este artículo y los lineales como "Lin" o simplemente sin denominación alguna. Tengo unos minipotes japoneses de 500K etiquetados como "B" que son más lineales que una flecha... en fin, un follón.

Lo mejor es comprobarlo con el polímetro. Si al 50% del recorrido da el 50% del valor podemos estar razonablemente seguros de que es lineal (o "Log-Antilog" pero esos, como veremos más tarde, son muy raros). Si no, lo más normal es que sean logarítmicos o de audio.

Para mayor complicación aún, los hay de audio de varios tipos, los que tienen el 30% del valor a mitad del recorrido (los he visto representados como "Log-A") y los que tienen el 10% a mitad de giro (los he visto como "Log-B") y luego los hay "Type-J", como los "HotPotz" que llevan los Wahs Crybaby, que tienen una respuesta logarítmica que gráficamente representada se asemeja a esa letra, los "Type-S" que son bilogarítmicos o "Log-Antilog" usados en ciertos osciladores (antiguamente se los etiquetaba como de tipo "F"), los "Seno-Coseno", Parabólicos etc, etc.

Pero no os preocupéis, que la cosa no es tan grave. A excepción de aplicaciones donde el "Taper" (respuesta) del pote sea muy importante, como en los Wahs, por ejemplo, siempre nos valdrá más o menos un tipo u otro. Quiero decir, valer... ¡vale!, lo que ocurre es que el resultado puede ser poco apropiado o incómodo. Por ejemplo, el mando de volumen de una guitarra (y en general de cualqueir cosa) ha de ser Logarítmico pues si es lineal, aunque también funcionará, la respuesta será muy "rara" y quedarán mal, por ejemplo, los "efectos violín".

Algunos equipos muy sofisticados de HiFi llevan en sus controles de "Balance" unos potenciómetros dobles especiales en los que uno de los componentes es "Antilog" y el otro es "Antilog Inverso", no "Log-Antilog" como a veces los llaman. Afortunadamente no nos hacen falta estas rarezas para nuestros montajes de pedales.

Y ya que hablamos de potes para guitarra... ¿que pasa con las guitarras para zurdos?. En un pote lineal lo único que habrá que hacer será invertir los cables de las patitas exteriores del pote y todo irá al revés, pero si es logarítmico... ¿cómo invertimos la forma de la curva para que la respuesta sea la correcta?.

De este truquito y de otros es de lo que vamos a tratar por aquí.

Modificación del valor de un Potenciómetro

Si no podemos encontrar un valor concreto de potenciómetro siempre podemos emplear un truquillo. Los potenciómetros son resistencias.... variables pero resistencias al fin y al cabo de modo que se les puede aplicar la misma fórmula de resistencias en paralelo:

1/Rtotal=1/R1 + 1/R2...

El caso más directo es que dos resistencias de igual valor puestas en paralelo dan como resultado una resistencia de la mitad de ese valor. Por ejemplo, si ponemos en paralelo dos resistencias de 100k (100000 Ohmios) obtendremos una resultante de 50K:

1/R = 1/100000 + 1/100000 => 1/R = 0.00001 + 0.00001 = 0.00002

R = 1/0.00002 = 50000 o, lo que es lo mismo, 50K.

Buen truco para dividir por dos el valor de un potenciómetro. Si tenemos un pote de 1M, si ponemos en paralelo una resistencia de ese mismo valor, esto es, una pequeña resistencia de 1/4W de 1M entre los terminales exteriores del potenciómetro (el central es, como ya sabemos el cursor), obtendremos un pote de 500K:

Esquema de resistencia puesta en paralelo con un potenciómetro.

Pero lo que es más interesante del caso es que no estamos obligados a que las resistencias sean idénticas entre sí. Podemos jugar con el valor de la resistencia añadida para conseguir el valor deseado. Por ejemplo y en el mismo caso anterior, si necesitamos un potenciómetro de un valor no estandard, por ejemplo de 30K:

1/R = 1/100000 + 1/68000 => 1/R = 0.00001 + 0.0000147 = 0.0000347

R = 1/0.0000347 = 28818.4, esto es, 28.8K lo que nos aproxima lo suficiente a las 30K que necesitamos.

Evidentemente nos tenemos que atener a los valores estandar que podamos encontrar para las resistencias. Si el valor fuese crítico, podríamos incluso poner un pequeño "trimmer" (potenciómetro de circuito impreso) en paralelo con nuestro potenciómetro principal y así conseguir el valor deseado con muchísima más precisión.

Trimmer

Respuestas (tapers) de potenciómetros

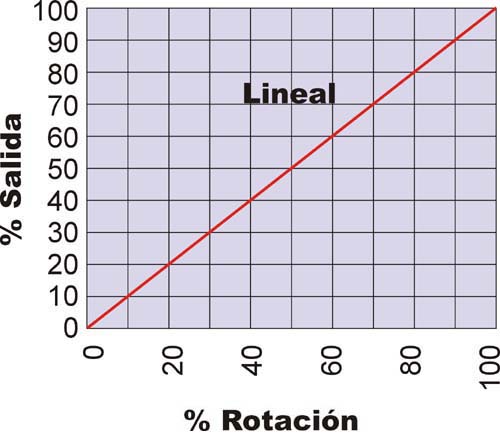
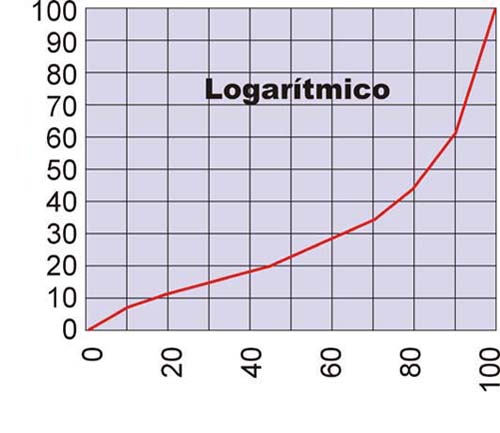
Aquí tenéis representadas las curvas de Variación (Taper) más comunes:

Gráfica de potenciómetro lineal (Tono) y logarítmico (Volumen).

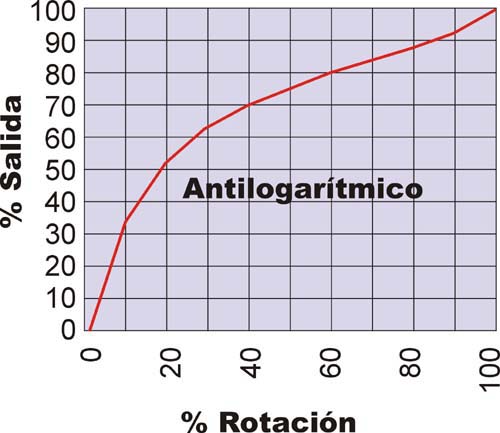
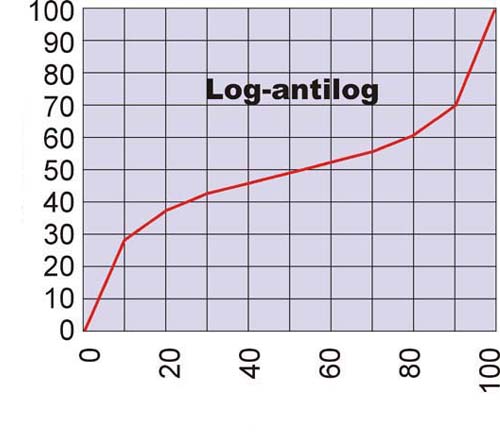
Gráfica de potenciómetro antilogarítmico y de log-antilog.

Fijáos detenidamente en las gráficas. Veréis que realmente las curvas están hechas con segmentos rectos. No son curvas auténticas. Esto está hecho deliberadamente pues en la realidad las curvas son así, pues es muchísimo más fácil y económico el hacer las pistas de los potes de este modo que si fuesen progresivos de un modo real. De hecho en la realidad no tienen más que dos o tres "rampas" con las que dibujar a "grosso modo" la curva final.

La verdad, el oído humano tampoco tiene tanta resolución para notar la diferencia, a excepción de el de Eric Johnson, claro.

Pues bien, nuestra intención es conseguir todos estos modos de una manera sencilla. Ya veremos para qué, pero por ahora os cuento el "por qué".

Los potenciómetros logarítmicos son caros. A igualdad de marca y modelo son más caros que los lineales pero lo que es peor es que la oferta es mucho menor. No hablo ya de los modelos esotéricos, como los "antilog" y los "log-antilog" ni mucho menos de rarezas como los "Seno-Coseno", que no hay quien los encuentre y si los hallas valen auténticas fortunas, sino de los mismos logarítmicos de audio de toda la vida. Si os fijáis en catálogos o preguntáis en vuestra tienda de electrónica favorita, lineales los hay en infinidad de valores, pero logarítmicos hay poquísimos. Normalmente de 10K, 47K, 100K, 220K y 470K cuando lineales los hay de muchísimas más variedades. ¿Qué pasa si queremos, por ejemplo, un potenciómetro de 25K Log?. Pues, una de dos, o nos volvemos locos buscando en catálogos extranjeros por correo y pagamos una pasta por ellos con gastos de envío incluídos.... o nos buscamos la vida con algún truquillo.

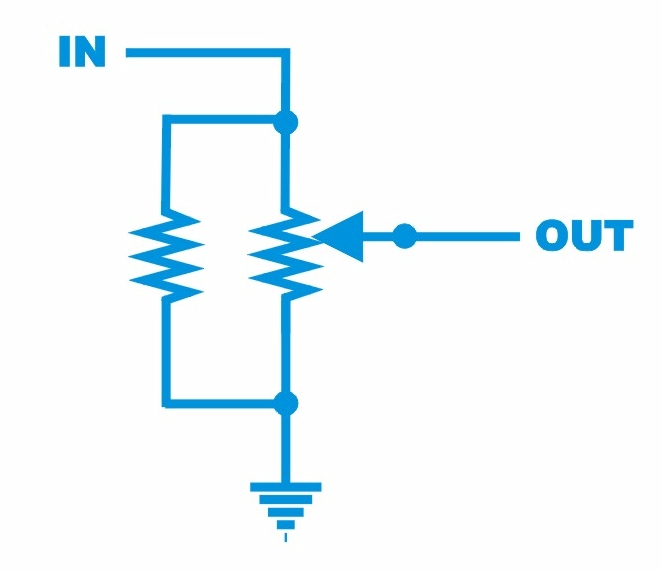
¡Al grano!... Ahora os cuento el "para qué". Si no encontramos o no queremos pagar demasiado por un pote logarítmico, podemos putilizar el truco de la resistencia de modificación de respuesta de potes (taper resistor). El truco es sencillísimo y funciona de maravilla. Se trata de añadir una resistencia del modo que se indica en el gráfico de más abajo. Esta resistencia ha de ser del 20% del valor nominal del potenciómetro lineal.

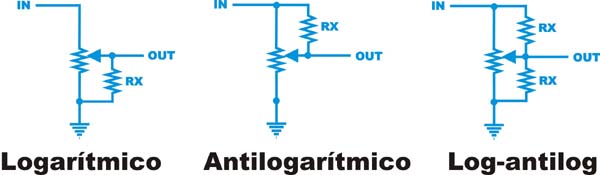
Por ejemplo, si necesitáis un potenciómetro de 100K Log y no lo encontráis, usad uno de 100K lineal y poned entre la patita de salida y la que va a masa (o la que va a la parte del circuito que va a masa) una resistencia de 20K. En el caso anterior, si necesitáis un pote de 25K logarítmico, como no los hay (los he buscado y no hay manera...) usad uno de 25K lineal y poned del mismo modo una resistencia de 5K. Sencillo ¿verdad?. Para las aplicaciones que aquí nos interesa podemos usar resistencias de esas pequeñitas de 1/4W.

Antes os hablaba de los zurdos... ¿os acordáis?. Los que no lo somos no nos podemos hacer bien a la idea de que incómodo que debe ser el que aunque nuestra guitarra sea zurda, que los potes funcionen "al derecho". Si os habéis encontrado en el caso y disponéis de una guitarra en la que los potes vayan "a la izquierda" y habéis tenido que cambiar alguno de volumen, sabréis de los que os hablo: dificilísimos de encontrar y carísimos. Solución: comprad uno lineal, cableadlo al revés y haced el truco del "Log", pero también al revés y obtendréis un pote Logarítmico "a izquierdas".... no lo confundáis con un Antilog, que no es lo mismo; fijáos en las gráficas. Así os ahorraréis un dineral y un montón de problemas.

Si queréis ver varias curvas diferentes con sus denominaciones japonesas echad un vistazo a este pdf de ALPS.

Modelo de Simulación

Hasta aquí todo va bien, pero ¿qué pasa si no nos restringimos a ese valor del 20% de la Resistencia de Variación que dije antes. Variando el valor de la resistencia de variación podréis cambiar la forma de la curva de respuesta.

Si queréis jugar con las posibilidades, bajáos la siguiente Hoja de Cálculo con la que podréis simular todo esto que os acabo de contar. Además os servirá de ayuda para comprenderlo si es que se os ha hecho un poco áspero.

TaperRes.xls. Formato Lotus Excel.

Aquí tienes un pantallazo de esa hoja de cálculo.
Pincha en la imagen para verla a tamaño completo.

No es oro todo lo que reluce...

Este truco desgraciadamente tiene un fallo. Aunque el resultado absoluto realmente se asemeja a lo emulado, la carga que vé la fuente anterior al pote, así como lo que vaya después de él no es la misma. De hecho es bastante menor. En esencia, tanto la carga que produce el potenciómetro a la circuitería previa así como la impedancia que "vé" lo que vaya después de él es de 1/5 de lo que sería si el potenciómetro fuese el real y no emulado.

Consecuentemente no deberemos usar este truco para evitar el tener que gastarnos algún euro más, sino cuando realmente nos sea imposible encontrar el potenciómetro real, aunque de hecho, casi siempre funcionará satisfactoriamente.

Todo esto que os acabo de contar es referido a cuando los potenciómetros son usados como tal. Si lo que necesitamos es variar la ley en un reostato, la cosa es más peliaguda. Cuando se usa como poteciómetro el cursor se desplaza entre dos "potenciales" diferentes, uno a cada extremo de la resistencia, pero cuando se usa como reostato no se da este caso.

Diferencias entre ambos tipos de uso. "n.c." es "No Conectado"

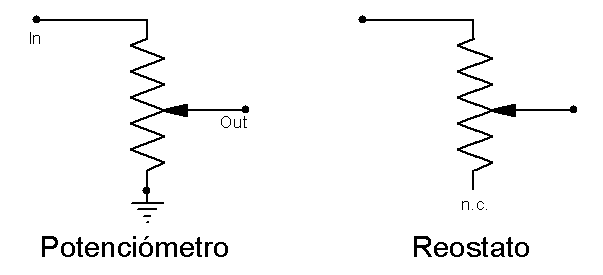
Si lo que necesitamos es modificar la ley de variación de un reostato tendremos que usar un método de resistencia de variación similar al usado con los potenciómetros pero con un par de diferencias significativas. El valor del potenciómetro ha de ser mayor y la resistencia de variación también. El método es el siguiente:

Los dos modelos sólo difieren en como empieza y acaba la curva.
El de la izquierda empieza el giro al 100% del valor final y el de la derecha empieza al 0% de ese valor, pero ambos con respuesta Antilogarítmica.

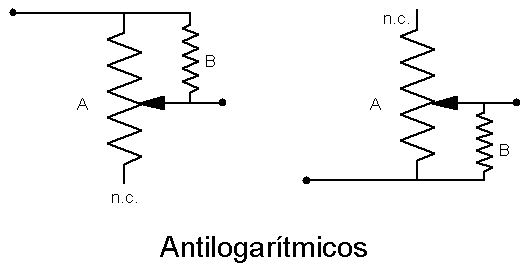
Para que el truco funcione necesitamos que el valor final del potenciómetro equivalente que queremos obtener sea un 20% del valor real de este y su resistencia de variación sea de un valor algo mayor que dicho valor real en aproximadamente otro 20%. De este modo, la resistencia equivalente de ambos en paralelo es más o menos igual al valor final que queremos. Como esto es un poco lioso vamos a un ejemplo con valores "redondos" para que quede claro:

Queremos obtener un potenciómetro antilogarítmico de 100K y no hay manera de encontrarlo. Para ello y siguiendo el método que acabo de contar compraremos un potenciómetro lineal de un valor tal que su 20% sean los 100K que queremos. Lo que necesitamos es un pote de 500K... el 20% de 500 es 100.

Para calcular la resistencia de variación necesitaremos comprar una que sea un 20% mayor que el valor final que queremos que tenga el pote resultante: 120K... el 20% de 100 es 20, luego 100 + 20 = 120.

En resumen, para obtener una "resistencia variable" de 100K de respuesta antilogarítmica necesitaremos un pote (A) de 500K, una resistencia (B) de 120K y montarlo todo según el gráfico "Antilogarítmico":

Este método tiene dos inconvenientes importantes:

• Sólo vale para leyes de variación Antilogarítmica. Es imposible obtener una respuesta Logarítmica de este modo.
  
  
• En la práctica sólo es factible para valores pequeños a causa de la necesidad de obtener potenciómetros lineales de un valor cinco veces mayor que el que necesitamos. Por ejemplo, para hacernos un "MXR Distorsion+" como es debido, el potenciómetro de ganancia ha de ser antilogarítmico de 1M, para lo cual, según este método, "B" debería ser una resistencia de 240K y "A" debería ser un pote de 5M!!!! Creedme que es difícil encontrar potes de más de 1M, lo que nos restringe en la práctica a valores que no sobrepasen los 200K.

Esta información está basada en un antiguo artículo de Jack Orman en AMZ que por alguna razón ya no está allí, pero sobre todo está basada en el extraordinario (aunque incompleto) artículo The Secret Life of Pots de, ¡cómo no!, R.G. Keen, en Better Volume (and Balance) Controls y en algunas cositas más que he investigado yo mismo.

©Piso-tones Ltd. Calambres | Guitarrista.com